Multiple regression is used when there are more than one predictors or input variables. It extends the simple linear regression model by giving each predictor a separate slope coefficient within a single model.
Given the number of predictors p equation is
![]()
![]() is the average effect on Y by increasing one of
is the average effect on Y by increasing one of ![]() , holding all the other predictors fixed.
, holding all the other predictors fixed.
![]() are called regression coefficients.
are called regression coefficients.
Computing Regression Coefficients
Regression coefficients are computed using the same least squares method as for simple linear regression models.
Choose ![]() to minimize the sum of squared residuals.
to minimize the sum of squared residuals.
![]()
Assessing Accuracy of Regression Coefficients
This is measured by answering the simple question is there a relationship between outcome variable and predictors.
Here we need to check whether all the regression coefficients are zero.
![]() (null hypothesis)
(null hypothesis)
![]() at least one
at least one ![]() is non-zero (alternative hypothesis)
is non-zero (alternative hypothesis)
Hypothesis test is performed by computing the F-statistics
![]()
Assessing Accuracy of Model (Model Fit)
Similar to simple linear regression RSE and ![]() are used in assessing the model fit.
are used in assessing the model fit.
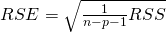
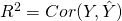
- In addition to RSE and
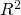 , it is recommended to plot the data and see if there are problems.
, it is recommended to plot the data and see if there are problems.
Assumptions in Multiple Linear Regression
Two main assumptions underlying the relationship between predictor variables and output variable
- Additive – effect of changes in a predictor variable on the output variable is independent from the values of other predictor variables
- Linear – change in output variable value by one unit of change in predictor variable is constant regardless of the value of the predictor variable
Other Assumptions
- Error terms,
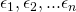 are uncorrelated
are uncorrelated - Error terms have constant variance,
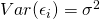
Extensions of Multiple Linear Regression
To accommodate non-linearity, a simple extension is polynomial regression.
Potential Problems and Remedies
1 Non-linearity of output-input variable’s relationships
Remedy:
- Residual Plots – Draw residual plots to identify non-linearity
- If non-linear, transform predictors to for example
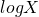 or
or 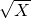 or
or 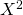
2 Correlation of error terms
This occurs often in time series data.
Remedy:
- To identify this plot residuals as a function of time. If it’s the case we can see tracking in the residuals that is adjacent residuals having the similar values.
3 Non-constant variance in error terms
Remedy:
- To identify this draw the residual plot and see if there is a funnel shape
- Transform the response/output Y using a concave function like
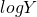 or
or 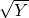
4 Outliers
- Draw residual plots to identify
- Better approach is to plot studentized residuals which is computed by dividing each residual
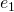 by its estimated standard error.
by its estimated standard error. - Remedy: Remove such observations
5 Collinearity
This means two or more predictor variables are closely related to each other.
Issues of collinearity
- Power of hypothesis test reduces
- Reduces the accuracy of regression coefficients
- Causes standard error to grow (this happens due to the reduced accuracy of regression coefficients)
- Result in decline in t-statistic
How to detect?
- Look at the correlation matrix of the predictors
- Compute variance inflation factor (VIF)
![]()
Rule of thumb: VIF > 5 or VIF > 10 indicates collinearity
Remedy:
- Drop one of the problematic variables from the model
- Combine collinear variables together into a single predictor variable