Classification methods are used when the output variable is qualitative. Predicting a qualitative outcome for an observation is referred to as ‘classifying’. Figure 1 presents some of the most widely used classification methods.

1. Logistic Regression
Logistic regression models the probability that an output variable (Y) belongs to a particular category. For example if you are modeling whether a patient is likely to develop diabetics or not, your output variable either belongs to yes or no category. So the logistic regression will looks at the probability that Y belongs to category ‘Yes’ and ‘No’.
To model an output variable we use the logistic function. Logistic function will always return a S-shaped curve.
Logistic function with a single predictor:
![]()
Computing Regression Coefficients
Model fitting is done by computing the maximum likelihood. It is a general approach to used for model fitting of non-linear models.
Likelihood function is given by the following equation.
![]()
Assessing Accuracy of Regression Coefficients
This is done by computing the standard errors as in linear regression models. Hypothesis testing is done using z-statistics similarly to the t-statistics used in linear regression setting.
Multiple Logistic Regression
Multiple logistic regression can be used when you have multiple predictor variables.
Logistic function with p number of predictors:
![]()
2. Linear Discriminant Analysis (LDA)
While logistic regression uses logistic function to model, linear discriminant analysis uses conditional distribution of the outcome variable Y. This means linear discriminant analysis draws conditional distribution for each predictor variable for each category separately and then uses Bayes’ theorem to compute final estimates.
Assumptions
- Shared variance across all K classes (
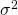 )
)
3. Quadratic Discriminant Analysis (QDA)
This is an alternative approach to linear discriminant analysis. However, it assumes each class has its own covariance matrix instead of sharing the same variance across all K classes as in linear discriminant analysis.
Comparison between LDA and QDA
LDA
- LDA is better if you have relatively few training observations
- Less flexible than QDA, yet has a lower variance
QDA
- Better if you have larger training set
- Suitable when variance is not a major concern