Model fitting refers to assessing the accuracy of the model. It is achieved by quantifying the extent to which model fits the data. The most common method in computing regression coefficients for model fitting is “least squares.” However to improve prediction accuracy and model interpretability, there are alternative model fitting methods too.
Prediction Accuracy
When number of observations are way greater than number of predictors, least squares tend to work well (n >> p). When p > n least squares can’t be used.
Remedy: Use shrinkage methods to constraint or shrink estimated coefficients.
Model Interpretability
Some of the predictor variables used in multiple regression may not be associated with the output variable. Removing such irrelevant variables improves the interpretation of the model. Removal of such variables can be done by setting the coefficient estimates to zero.
Model Fitting Approaches
- Subset Selection
- Shrinkage
- Dimension Reduction
1. Subset Selection
In this method, we identify a subset of the p predictors that we think are relevant and do the modeling fitting using least squares. There are two approaches to subset selection.
I. Best Subset Selection
In this approach we fit a separate least squares regression for each possible combination (
) of p predictors.
Drawbacks: Can’t apply when p is very large. May lead to overfitting or high variance of coefficient estimates.
II. Stepwise Selection
A computationally efficient approach than best subset selection. Instead of looking at all possible models, it starts with either a no predictor and keep on adding predictors or with p predictors and keep on removing.
This includes two methods: forward stepwise selection and backward stepwise selection.
a. Forward Stepwise Selection
We begin with 0 predictors and then keep on adding predictors one-at-a-time, until all the predictors are in the model.
Can be used in both occasions when n > p and n < p.
b. Backward Stepwise Selection
We begin with all p predictors and then removing one-at-a-time.
Requires n > p
Assessing Accuracy of Model (Model Fit)
RSS and 
are not suitable for assessing model accuracy when there are different number of predictors in each model. To choose the best model we need to compute the test error as explained in previous blog posts.
There are two main approaches to calculate test error in the best subset selection setting.
1. Indirectly compute test error by making an adjustment to the training error to account for bias due to overfitting
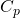
- Akaike Information Criterion (AIC)
- Bayesian Information Criterion (BIC)
- Adjusted
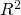
2. Directly compute test error using a validation set or cross-validation approach
- Compute validation set error or cross-validation error for each model and select te smallest test error
2. Shrinkage Methods
This is an approach which we can use to shrink coefficient estimates towards zero by constraining or regularizing coefficients. Shrinking coefficients results in reduced variance. The two of the common shrinkage methods are ridge regression and lasso. These two can also be viewed as improved linear models by reducing the complexity.
I. Ridge Regression
This is similar to using least squares. The objective is to make RSS small, so that the model fits the data. Therefore, ridge regression introduces tuning parameter and shrinkage penalty to estimate coefficients towards zero. In least squares setting, it generates only a one set of coefficients. However, in this approach, it returns a different set of coefficients estimates for each value of tuning parameter. The value for tuning parameter is chosen using the cross-validation approach.
Drawbacks
- Includes all predictor variables in the final model. It doesn’t exactly make coefficients to zero. However, this is not an issue for accuracy.
- Interpretability becomes challenging, when you have predictor variables almost close to 0 in the presence of large number of predictor variables.
II. Lasso
This is similar to ridge regression except that tuning parameter can force to make coefficient estimates to zero.
Advantages
- Shirnks coefficient estimates to be exactly 0
- Much easier to inpret than ridge regression models
- Returns sparse models that have only a subset of predictor variables
3. Dimension Reduction Methods
In this approach, predictor variables are transformed and then fitted to least squares model. The main target is to estimate lesser number of coefficients (M) which is M < p.
Principle component regression (PCR) and partial least squares (PLS) are some of the popular approaches for deriving low-dimensional set of predictors. These two can also be viewed as improved linear models by reducing the complexity.
I. Principle Component Regression (PCR)
In principle component analysis (PCA), when we plot an output variable with a predictor variable, the first principle component defines the line that represents as close as possible to the data. The maximum number of distinct components that we can have is equal to number of predictors.
In this approach, we construct the first M principle components and we use these components as predictors to fit a linear regression model using least squares. The number of principle components that we use in the model are decided using cross-validation approach. If the predictor variables are measured in different units, then we need to standardize the predictor variables.
Drawbacks
- Identifies directions in an unsupervised way without using the output variable. That is output doesn’t supervise the identification of principle components.
- There is no guarantee predictions will be on the same direction
II. Partial Least Squares (PLS)
This is a supervised alternative to PCR. This method uses both predictors and output variable to find directions. Predictor variables should be standardized. This approach may reduce the bias, however it is possible that it may increase the variance.
High Dimensional Setting
When there are large number of predictor variables with small number of observations, we call it a “high dimensional” problem. Dimension here refers to the size of p.
p >> n : high dimensional (data sets containing more predictors than observations)
p << n : low dimensional (data sets containing less predictors than observations)
Problems in High Dimensional Setting
- Can’t use 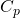, AIC, and BIC
- Can’t use adjusted
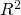
- Multicollinearity gets worse
- Should not use sum of squared errors, p-values, 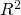for model fit on training data
Regression in High Dimensional Setting
- Can use forward stepwise selection, ridge regression, principle component regression and lasso
- Report results on an independent test data set rather on the training data set (MSE or 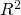) or on cross-validation errors
Curse of Dimensionality
This occurs when the number of predictors increase. That is when p increases, quality of the fitted model decreases. While having truly associated predictors reduces the test error, noisy predictors deteriorate the quality of the fitted model by increasing test error.